RU descriptives

#start with clean workspace 
rm(list=ls())
getwd()

#> [1] "C:/Users/ninab/OneDrive/Documenten/GitHub/labjournal"

1 packages

library(data.table) 
library(tidyverse) 
require(stringi)
require(Rsiena)
require(igraph)

2 Data

#load dataobjects
load("./data/descriptives/RU_net_array_sym.RData")
load("./data/descriptives/RU_dfv2.RData")

3 custum functions

# density: observed relations divided by possible relations
fdensity <- function(x) {
    # x is your nomination network make sure diagonal cells are NA
    diag(x) <- NA
    # take care of RSiena structural zeros, set as missing.
    x[x == 10] <- NA
    sum(x == 1, na.rm = T)/(sum(x == 1 | x == 0, na.rm = T))
}

# calculate intragroup density
fdensityintra <- function(x, A) {
    # A is matrix indicating whether nodes in dyad have same node attributes
    diag(x) <- NA
    x[x == 10] <- NA
    diag(A) <- NA
    sum(x == 1 & A == 1, na.rm = T)/(sum((x == 1 | x == 0) & A == 1, na.rm = T))
}

# calculate intergroup density
fdensityinter <- function(x, A) {
    # A is matrix indicating whether nodes in dyad have same node attributes
    diag(x) <- NA
    x[x == 10] <- NA
    diag(A) <- NA
    sum(x == 1 & A != 1, na.rm = T)/(sum((x == 1 | x == 0) & A != 1, na.rm = T))
}

# construct dyadcharacteristic whether nodes are similar/homogenous
fhomomat <- function(x) {
    # x is a vector of node-covariate
    xmat <- matrix(x, nrow = length(x), ncol = length(x))
    xmatt <- t(xmat)
    xhomo <- xmat == xmatt
    return(xhomo)
}

# a function to calculate all valid dyads.
fndyads <- function(x) {
    diag(x) <- NA
    x[x == 10] <- NA
    (sum((x == 1 | x == 0), na.rm = T))
}

# a function to calculate all valid intragroupdyads.
fndyads2 <- function(x, A) {
    diag(x) <- NA
    x[x == 10] <- NA
    diag(A) <- NA
    (sum((x == 1 | x == 0) & A == 1, na.rm = T))
}

4 descriptives

summary(soc_df$div.net)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
#>    0.00    0.00   15.48   23.61   37.24  100.00       2

sd(soc_df$div.net, na.rm=TRUE)

#> [1] 27.7464

table(soc_df$div.net)

#> 
#>     0  4.17  6.98  9.09 13.79 14.29 16.67 18.75  22.5    25 28.57 28.95    40 42.86    60    70 
#>    10     1     1     1     1     1     2     1     1     1     1     1     2     1     1     1 
#> 71.43 78.57   100 
#>     1     1     1

hist(soc_df$div.net, col="lightblue", main='RU: ethnic diversity egonets', xlab='Percentage non-Dutch collaborators')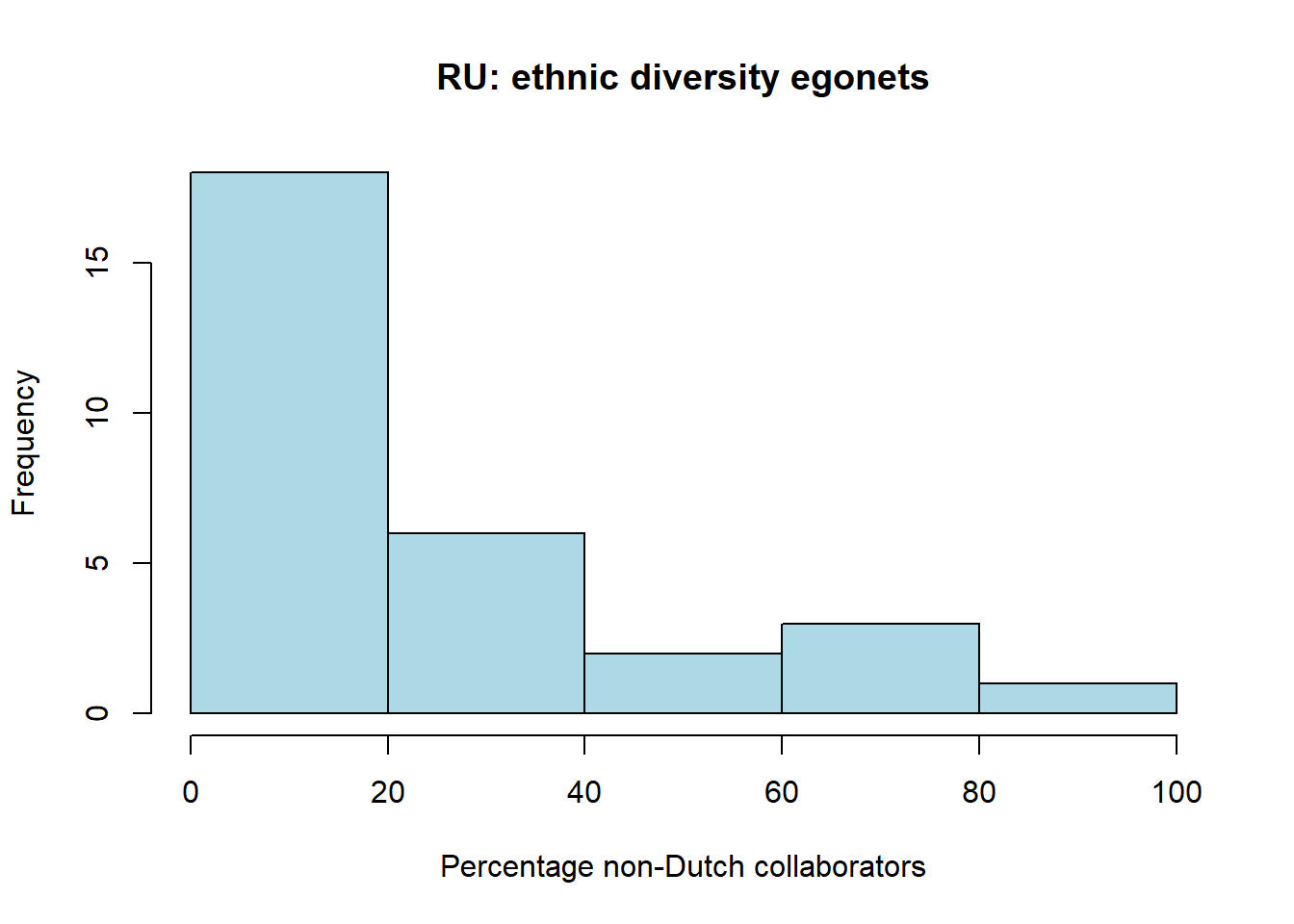

summary(soc_df$div.ego)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>  0.0000  1.0000  1.0000  0.8438  1.0000  1.0000

table(soc_df$div.ego)

#> 
#>  0  1 
#>  5 27

summary(soc_df$nauthors)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
#>     1.0     5.5    11.0    13.1    15.0    43.0       1

sd(soc_df$nauthors, na.rm=TRUE)

#> [1] 11.06452

hist(soc_df$nauthors, col="lightblue", main='RU: number of co-authors', xlab='Number of co-authors since 2019')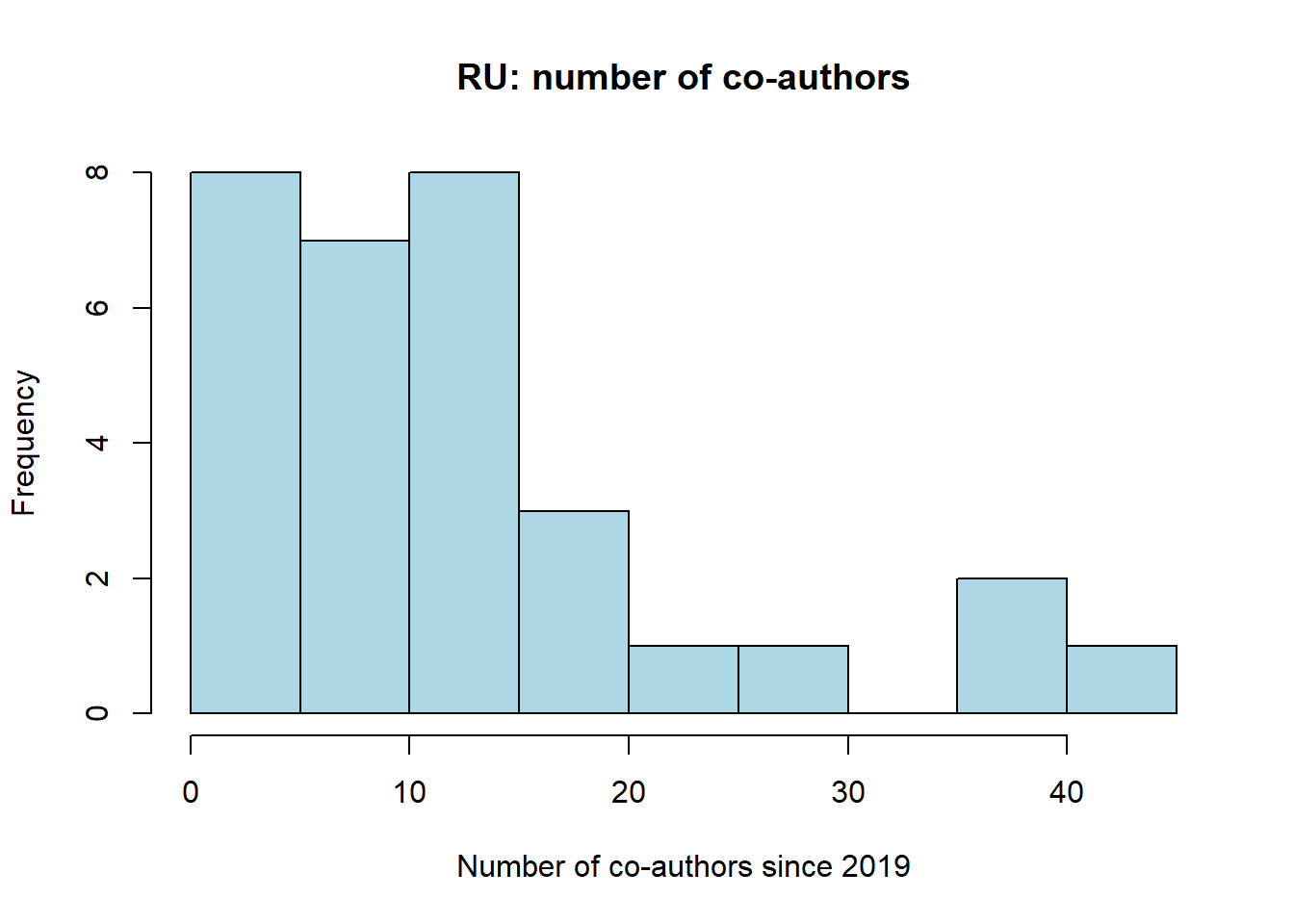

summary(soc_df$pub_first)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    1970    2005    2011    2007    2017    2019

sd(soc_df$pub_first, na.rm=TRUE)

#> [1] 13.59254

hist(soc_df$pub_first, col="lightblue", main='RU: year first publication', xlab='Year first publication')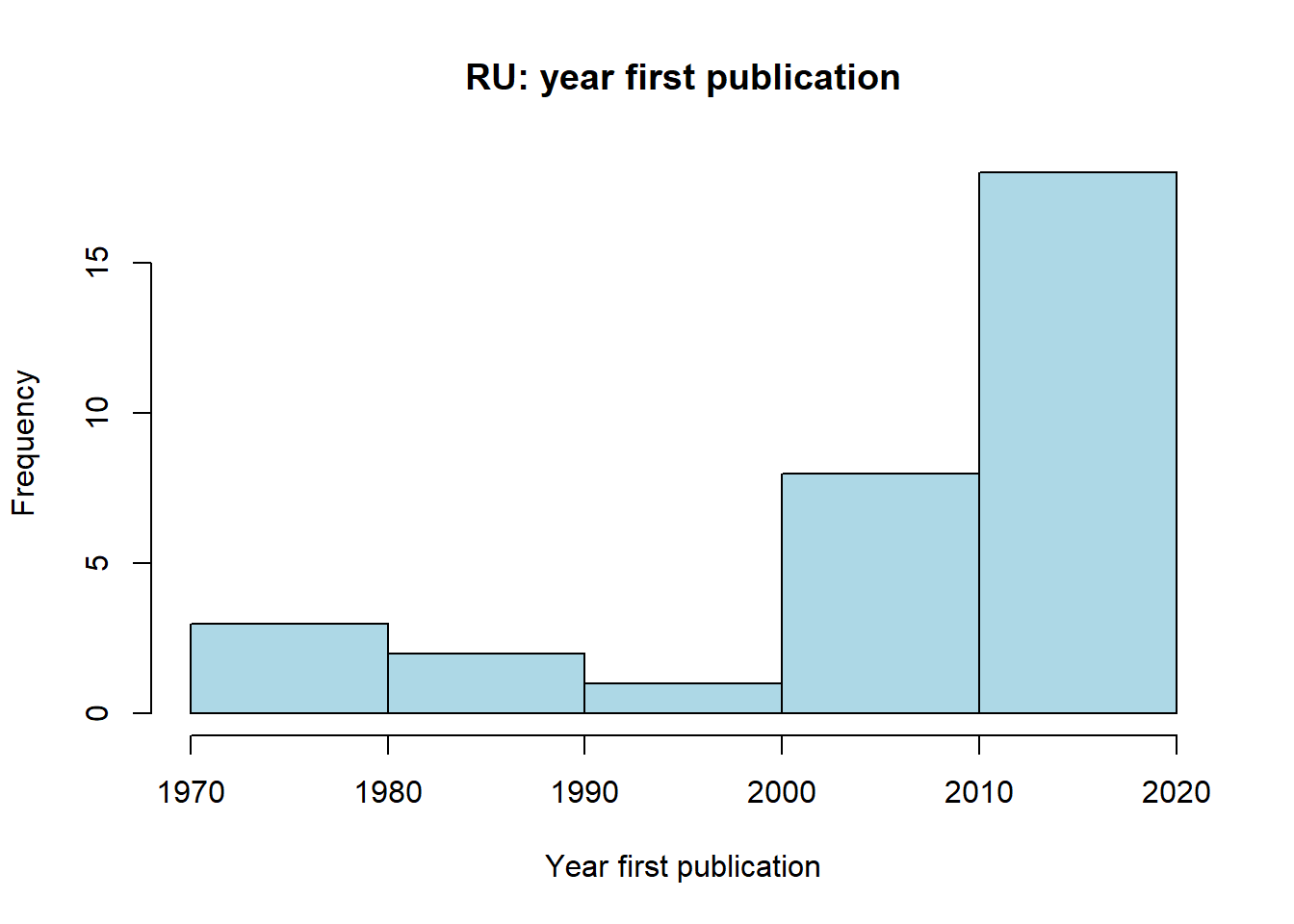

table(soc_df$gender4)

#> 
#>  0  1 
#> 16 16

hist(soc_df$gender4, col="lightblue")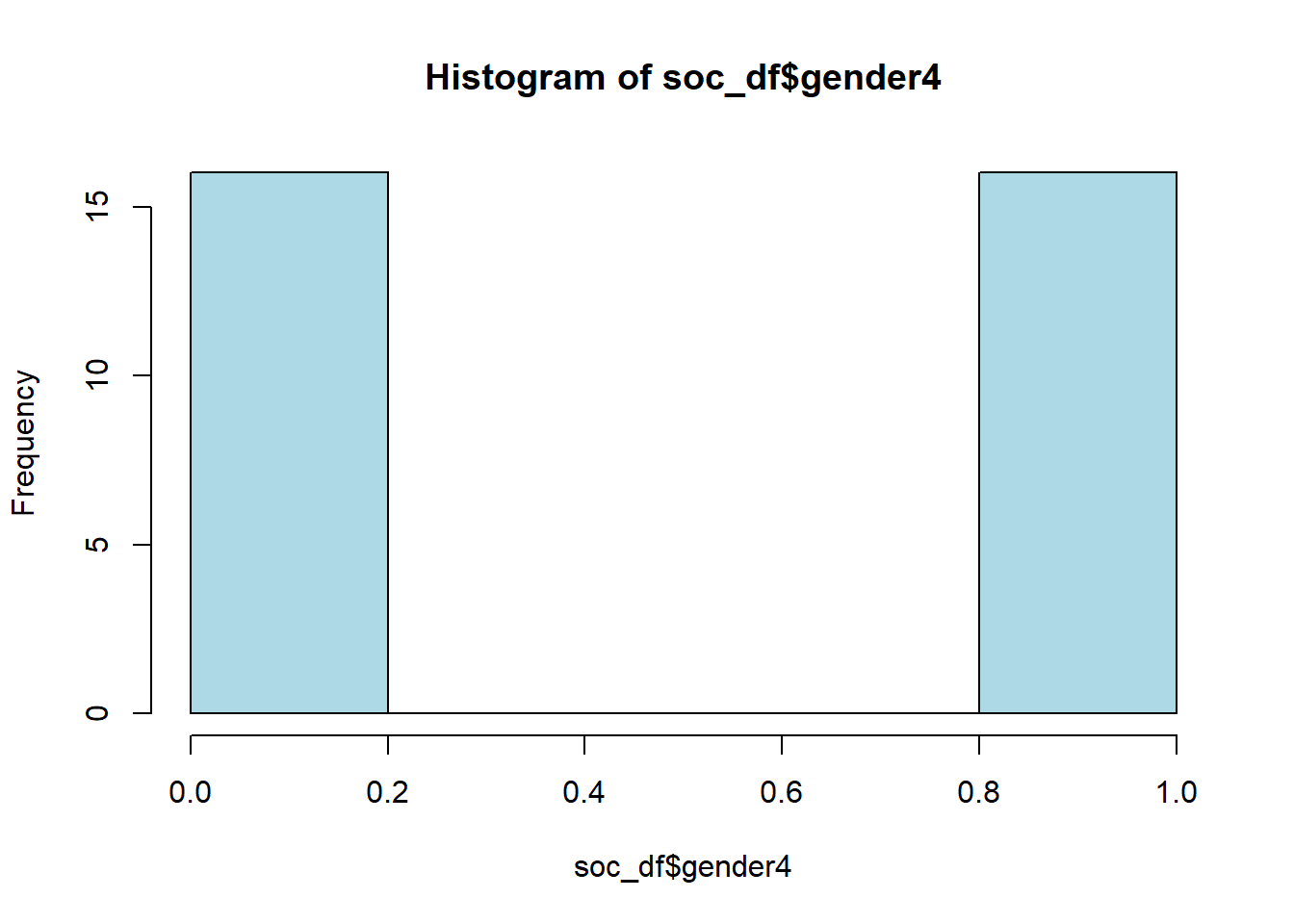

5 degree

5.1 net 1

net1 <- net_soc_array[ ,, 1]
diag(net1) <- 0
degree <- rowSums(net1)
hist(degree)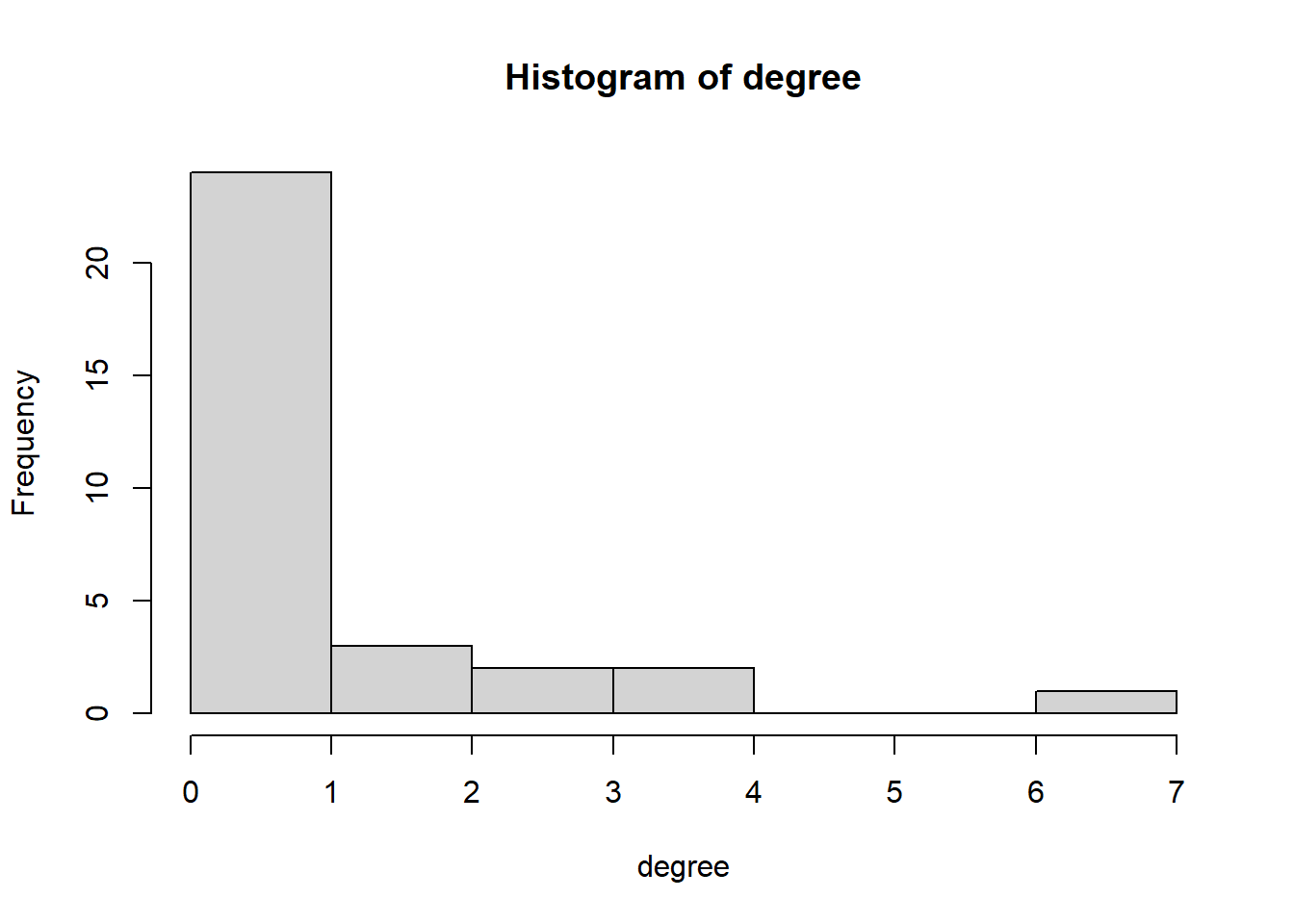

summary(degree)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>  0.0000  0.0000  0.0000  0.9375  1.2500  7.0000

sd(degree)

#> [1] 1.66438

5.2 net 2

net2 <- net_soc_array[ ,, 2]
diag(net2) <- 0
degree <- rowSums(net2)
hist(degree)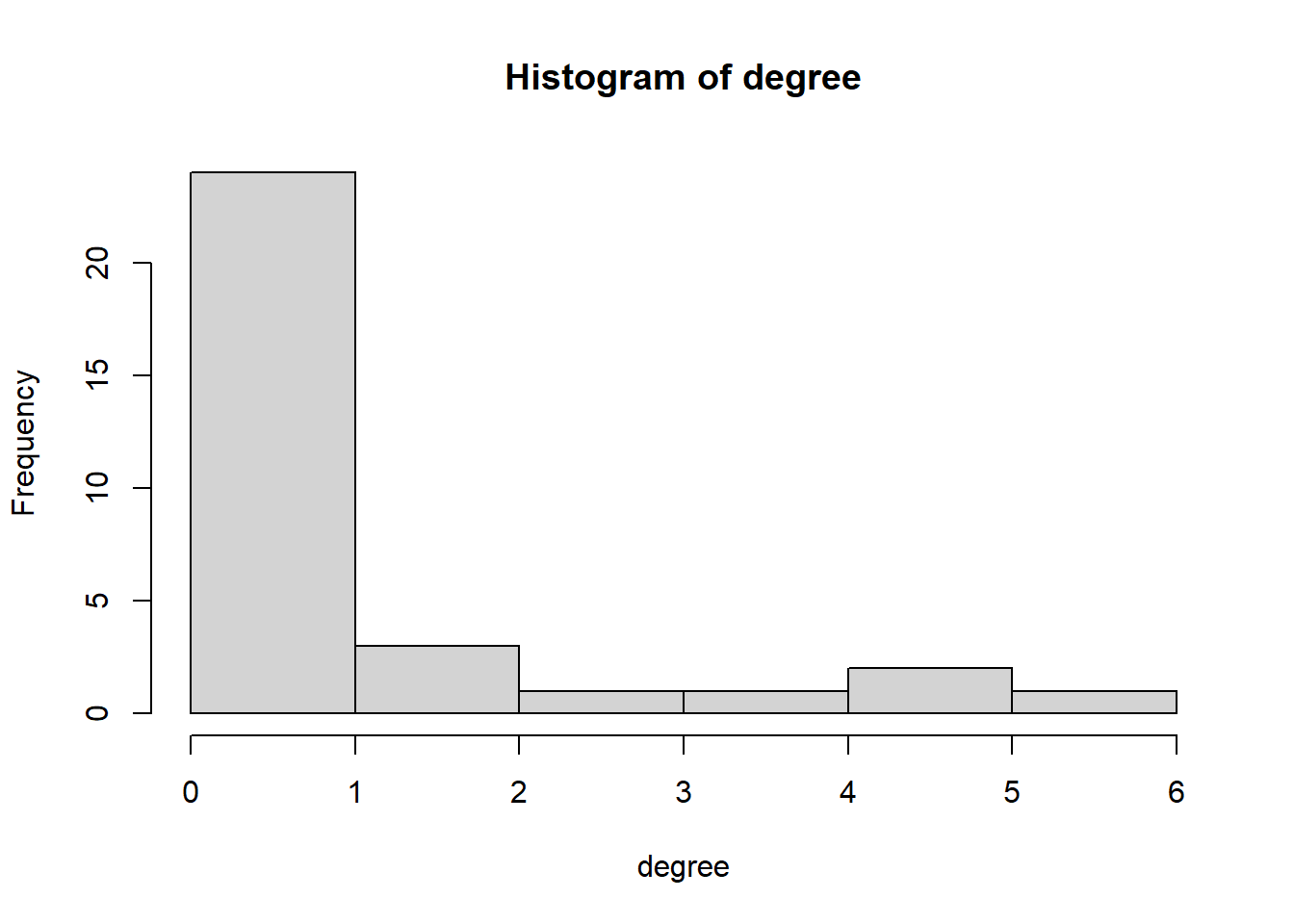

summary(degree)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>   0.000   0.000   0.000   1.062   1.250   6.000

sd(degree)

#> [1] 1.721543

5.3 net 3

net3 <- net_soc_array[ ,, 3]
diag(net3) <- 0
degree <- rowSums(net3)
hist(degree)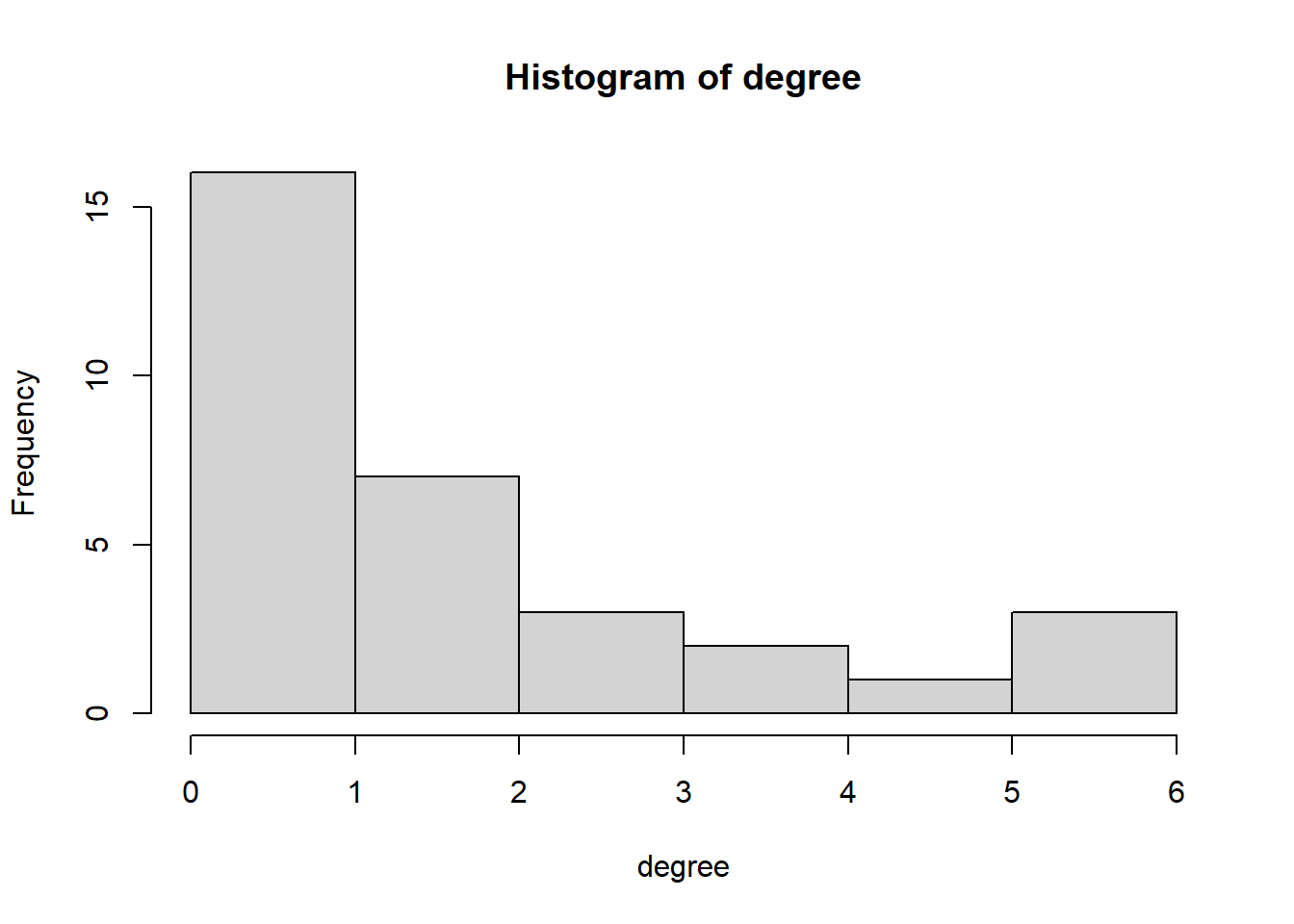

summary(degree)

#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    0.00    0.00    1.50    1.75    3.00    6.00

sd(degree)

#> [1] 2

6 igraph object

6.1 net 1

net1_g <- igraph::graph_from_adjacency_matrix(net1, mode = c("undirected"))
plot(net1_g)

igraph::degree(net1_g)

#>  [1] 0 0 0 0 0 0 4 0 0 0 1 0 0 7 2 1 2 0 3 2 3 4 0 0 0 0 0 0 0 1 0 0

igraph::dyad.census(net1_g)

#> $mut
#> [1] 15
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 481

igraph::triad.census(net1_g)

#>  [1] 4546    0  384    0    0    0    0    0    0    0   24    0    0    0    0    6

igraph::edge_density(net1_g)

#> [1] 0.03024194

sum(igraph::degree(net1_g))

#> [1] 30

6.2 net 2

net2_g <- igraph::graph_from_adjacency_matrix(net2, mode = c("undirected"))
plot(net2_g)

igraph::degree(net2_g)

#>  [1] 1 0 0 0 2 0 5 0 2 1 0 0 0 6 1 1 5 2 1 0 4 3 0 0 0 0 0 0 0 0 0 0

igraph::dyad.census(net2_g)

#> $mut
#> [1] 17
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 479

igraph::triad.census(net2_g)

#>  [1] 4492    0  431    0    0    0    0    0    0    0   32    0    0    0    0    5

igraph::edge_density(net2_g)

#> [1] 0.03427419

sum(igraph::degree(net2_g))

#> [1] 34

6.3 net 3

net3_g <- igraph::graph_from_adjacency_matrix(net3, mode = c("undirected"))
plot(net3_g)

igraph::degree(net3_g)

#>  [1] 0 0 0 0 2 0 6 1 1 0 0 0 0 6 2 3 5 6 3 4 2 2 2 0 0 2 2 4 3 0 0 0

igraph::dyad.census(net3_g)

#> $mut
#> [1] 28
#> 
#> $asym
#> [1] 0
#> 
#> $null
#> [1] 468

igraph::triad.census(net3_g)

#>  [1] 4192    0  707    0    0    0    0    0    0    0   50    0    0    0    0   11

igraph::edge_density(net3_g)

#> [1] 0.05645161

sum(igraph::degree(net3_g))

#> [1] 56

7 density

7.1 net 1

net_und <- net1 + t(net1)
net_und[net_und==2] <- 1

sum(net_und, na.rm=TRUE)

#> [1] 30

fdensity(net1)

#> [1] 0.03024194

7.2 net 2

net_und <- net2 + t(net2)
net_und[net_und==2] <- 1

sum(net_und, na.rm=TRUE)

#> [1] 34

fdensity(net2)

#> [1] 0.03427419

7.3 net 3

net_und <- net3 + t(net3)
net_und[net_und==2] <- 1

sum(net_und, na.rm=TRUE)

#> [1] 56

fdensity(net3)

#> [1] 0.05645161

8 inter-/intragroup density

div_m <-  fhomomat(soc_df$div.ego)

# calculate intra-/intergroup density diversity ego
fdensityintra(x=net_und, A=div_m) 

#> [1] 0.06371191

fdensityinter(x=net_und, A=div_m)

#> [1] 0.03703704

# calculate intra-/intergroup density gender
gender_m <-  fhomomat(soc_df$gender4)
fdensityintra(x=net_und, A=gender_m) 

#> [1] 0.05833333

fdensityinter(x=net_und, A=gender_m)

#> [1] 0.0546875